Appendix A. Some basic computations between reference and real elements¶
Volume integral¶
One has

Denoting  the jacobian
the jacobian

one finally has

When  , the expression of the jacobian reduces to
, the expression of the jacobian reduces to  .
.
Surface integral¶
With  a part of the boundary of
a part of the boundary of 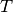 a real element and
a real element and
 the corresponding boundary on the reference element
the corresponding boundary on the reference element  ,
one has
,
one has

where  is the unit normal to
is the unit normal to  on
on  . In a same
way
. In a same
way

For  the unit normal to
the unit normal to 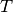 on
on  .
.
Second derivative computation¶
Denoting
![\nabla^2 f =
\left[\frac{\partial^2 f}{\partial x_i \partial x_j}\right]_{ij},](../_images/math/922650db95a714a428af3c384a4e359d258de17e.png)
the  matrix and
matrix and

the  matrix, then
matrix, then

and thus

In order to have uniform methods for the computation of elementary matrices, the
Hessian is computed as a column vector  whose components are
whose components are
 . Then, with
. Then, with
 the
the  matrix defined as
matrix defined as
![\left[B_2(\widehat{x})\right]_{ij} =
\sum_{k = 0}^{N-1}
\frac{\partial^2 \tau_k(\widehat{x})}{\partial \widehat{x}_{i / P} \partial \widehat{x}_{i\mbox{ mod }P}}
B_{kj}(\widehat{x}),](../_images/math/af0dc2d4ddff4d7e7c23ea66da969f7cd3547afb.png)
and  the
the  matrix defined as
matrix defined as
![\left[B_3(\widehat{x})\right]_{ij} =
B_{i / N, j / P}(\widehat{x}) B_{i\mbox{ mod }N, j\mbox{ mod }P}(\widehat{x}),](../_images/math/a154bfb20b9d7666d4d1ac1dc4f0ea257870ff0d.png)
one has

Example of elementary matrix¶
Assume one needs to compute the elementary “matrix”:

The computations to be made on the reference elements are

and

Those two tensor can be computed once on the whole reference element if the
geometric transformation is linear (because  is constant). If the
geometric transformation is non-linear, what has to be stored is the value on
each integration point. To compute the integral on the real element a certain
number of reductions have to be made:
is constant). If the
geometric transformation is non-linear, what has to be stored is the value on
each integration point. To compute the integral on the real element a certain
number of reductions have to be made:
- Concerning the first term (
 ) nothing.
) nothing. - Concerning the second term (
 ) a
reduction with respect to
) a
reduction with respect to  with the matrix
with the matrix 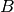 .
. - Concerning the third term (
 )` a reduction of
)` a reduction of  with respect to
with respect to  with the matrix
with the matrix  and a reduction of
and a reduction of  with respect also
to
with respect also
to  with the matrix
with the matrix 
The reductions are to be made on each integration point if the geometric transformation is non-linear. Once those reductions are done, an addition of all the tensor resulting of those reductions is made (with a factor equal to the load of each integration point if the geometric transformation is non-linear).
If the finite element is non- -equivalent, a supplementary reduction of the
resulting tensor with the matrix
-equivalent, a supplementary reduction of the
resulting tensor with the matrix  has to be made.
has to be made.

